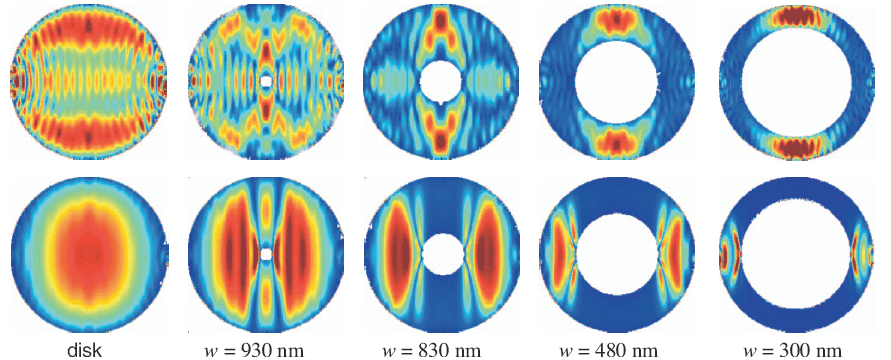
If the outer shape of a finite-size magnet deviates from an ellipsoid the internal field becomes spatially inhomogeneous. This is often found in case of nanopatterned magnonic devices. The inhomogeneity appears regardless if saturated or non-saturated magnets are considered. The internal field enters the equation of motion of the spins. Thereby, both, the wave vectors and/or the eigenfrequencies of  spin waves can vary from position to position. If compared to electromagnetic waves (photons) one can say that the inhomogeneous internal field varies the refractive index for spin waves.  The variation gives rise to interesting localization phenomena on the nanoscale. The localization length can be far smaller than the geometrical size of the magnonic device. At the same time, quantization effects  might occur due to the geometrical boundaries. For spin waves in nanomagnets, the exact boundary conditions are still under investigation. They depend crucially on the spin-wave pattern, ferromagnetic material, edge geometry and roughness. We have fabricated Permalloy rings with different radii of the central hole but fixed outer radius to explore the localization phenomena in mesoscopic magnets with a tailored magnetic configuration.

Eigenmodes (simulations) of a disk and rings with different centrol hole radius at high (upper row) and low frequency (bottom row). The width w of the ring arms are given. Red (blue) color depicts large (zero) spin precession amplitude.